小学生算数の苦手克服！「速さ」をマスターして中学受験も乗り越えよう！

小学生の算数の中で、最も苦手とする人が多いのが「速さ」の単元です。図形や計算問題と比べて、イメージしにくく、複雑な思考を要するために、多くの子どもたちがつまづきやすい単元となっています。

しかし、「速さ」は中学受験でも頻出の重要単元です。さらに、中学校で数学を勉強する上でも大切な基礎となります。日常生活でも、電車の時刻表を読んだり、旅行の計画を立てたりする際に役立つ知識です。

そこで、今回のコラムでは「速さ」の概念を徹底的に解説し、つまずきやすいポイントを克服する方法を紹介します。基本から応用まで、段階的に理解を深めていきましょう。

「速さ」で習うこと
- 速さの意味や単位
- 公式
なぜ「速さ」が苦手になるのか
「速さ」の問題を克服するポイントと勉強法
「速さ」についての練習問題
- 基本問題
応用問題
苦手単元「速さ」の克服術まとめ

「速さ」で習うこと

車のスピードメーター

速さの意味や単位

「速さ」とは、単位時間あたりにどれだけ進むかを表す概念です。主に以下の3つの単位で表されます：

時速（km/h）: 1時間あたりに進む距離をキロメートルで表します。例：時速60km（1時間に60km進む）
分速（m/分）: 1分間あたりに進む距離をメートルで表します。例：分速100m（1分間に100m進む）
秒速（m/秒）: 1秒間あたりに進む距離をメートルで表します。例：秒速10m（1秒間に10m進む）

これらの単位は状況に応じて使い分けます。例えば、車や電車の速さは時速で、人の歩く速さは分速で、短距離走の速さは秒速で表すことが多いです。

公式

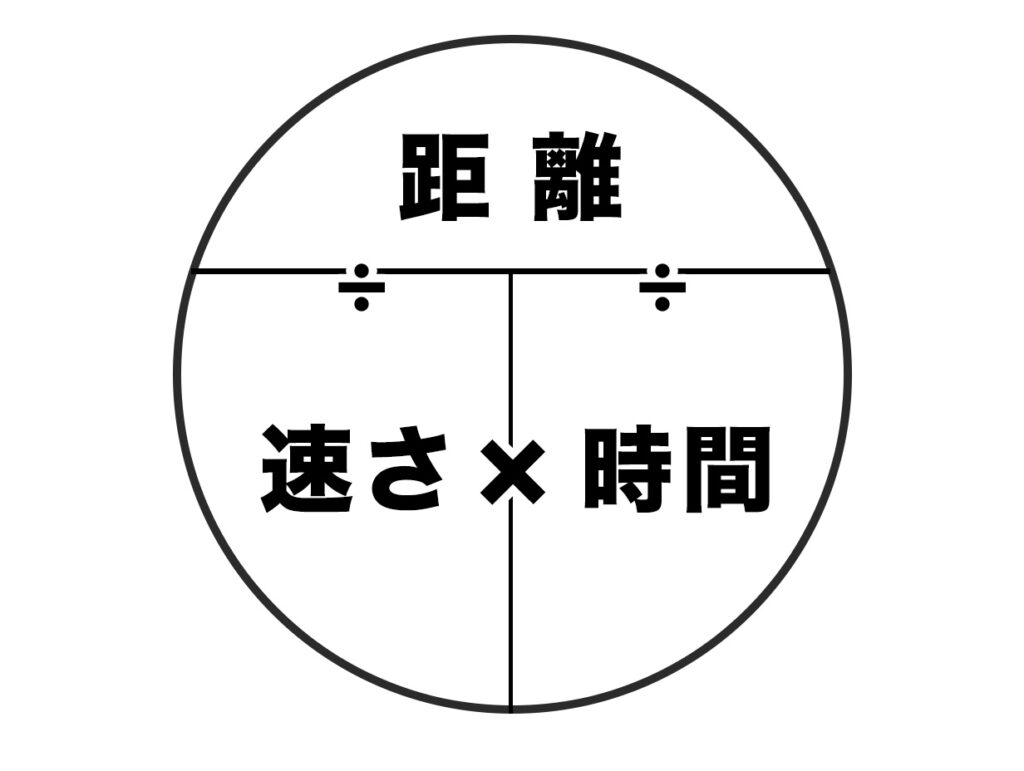
速さの公式の図

速さに関する基本的な公式は以下の3つです：

速さ = 距離 ÷ 時間
距離 = 速さ × 時間
時間 = 距離 ÷ 速さ

これらの公式を覚えておくと、様々な問題に対応できます。ただし、単に暗記するだけでなく、その意味を理解することが重要です。

関連記事：成績アップを！おすすめの勉強方法を紹介！算数・数学編

なぜ「速さ」が苦手になるのか

速さが苦手な学生

「速さ」の単元が多くの小学生にとって苦手意識の対象となる理由には、いくつかの要因があります。

公式を暗記するだけでは攻略できない

速さの基本公式「速さ = 距離 ÷ 時間」を覚えることは簡単ですが、単に暗記するだけでは多くの問題に対応できません。速さの問題には、2つの物体が出会う問題や追いつき問題などがあり、状況に応じた考え方が求められます。

また、問題文から距離・時間・速さを正確に読み取る力や、公式の変形「距離 = 速さ × 時間」「時間 = 距離 ÷ 速さ」を適切に使うことも重要です。
多くの場合、1つの公式を適用するだけでは問題が解けず、複数のステップを踏んで解答にたどり着く必要があります。このため、問題の状況を頭の中で絵や図にイメージする力も重要になってきます。

単位の変換でミスしやすい

速さの問題では、しばしば単位の変換が必要になります。多くの小学生がここで戸惑い、つまづく原因となりやすいです。。距離や時間、速さには様々な単位があり、問題に応じて正確な変換が必要です。例えば、時速をm/s（秒速）に直す際は1000m/3600sといった計算や、また、分速80mを時速に直す場合、80 × 60 = 4800m/h = 4.8km/hという2段階の変換が必要です。

さらに、「分速」と聞いて「1分間に進む距離」と「1時間に進む距離」を混同してしまうなど、概念理解が不十分な場合もあり、計算ミスが答えに影響します。正確な単位変換を確実に行えるようになることが、速さの問題を解く上で非常に重要です。

割合や比の考え方が身についていない

速さの問題は、割合や比の概念と密接に関連しています。速さは「単位時間あたりの距離」であり、割合そのものです。

例えば「分速80m」は「1分あたり80mの割合」と解釈できます。速さの比較や変化には比の考え方が必要で、「AさんはBさんの1.2倍の速さで走る」という表現は、比の概念を用いています。また速さが20%増える場合などは割合の理解が求められます。

このように、速さの概念を深く理解し、様々な問題に対応するためには割合や比の基本的な概念をしっしりと理解しておくことが重要です。

「速さ」の問題を克服するポイントと勉強法

速さの概念を勉強する中学生

基本をしっかり押さえる：速さ、距離、時間の関係を表す基本公式をしっかり理解しましょう。公式の意味を考え、なぜそうなるのかを理解することが大切です。
単位変換を習得する：時速、分速、秒速の変換や、キロメートルとメートルの変換などを繰り返し練習しましょう。変換表を作成して、常に参照できるようにするのも良い方法です。
問題文を図や表に整理してみる：問題文がうまく理解できない場合、与えられた情報を図や表に整理してみましょう。これにより、問題の全体像が把握しやすくなります。
パターンを理解する：追いつき問題、往復問題、平均の速さなど、よく出題されるパターンを理解し、それぞれの解き方を習得しましょう。
定期的に復習する：習得した内容を定期的に復習しましょう。特に、苦手だと感じる問題タイプは重点的に取り組みましょう。
段階的に難易度を上げる：基本問題から始めて、徐々に難易度を上げていきましょう。無理をせず、着実に理解を深めていくことが大切です。
日常生活と結びつける：電車の時刻表や旅行計画など、日常生活で速さの概念を意識的に活用してみましょう。実生活との結びつきを感じることで、理解が深まります。

関連記事：数学のケアレスミスをなくすには？原因と対策をプロが解説

「速さ」についての練習問題

歩く速度1

理解を深めるために、いくつかの練習問題に取り組んでみましょう。

基本問題

問題1：1500mを25分間で歩きました。分速何mでしょうか。
問題2：分速75mで15分歩きました。何m歩いたでしょうか。
問題3：1800mを分速90mで歩きました。何分かかったでしょうか。

解説

問題1

問題文の情報：距離 = 1500m、時間 = 25分
求めるもの：速さ（分速）
使用する公式：速さ = 距離 ÷ 時間

計算：1500 ÷ 25 = 60

答え：分速60m

解説：1500mを25分で歩いたということは、1分あたりの距離を求めればよいことがわかります。全体の距離を時間で割ることで、1分あたりの距離（速さ）が求められます。

歩く速度2

問題2

問題文の情報：速さ = 分速75m、時間 = 15分
求めるもの：距離
使用する公式：距離 = 速さ × 時間

計算：75 × 15 = 1125

答え：1125m

解説：1分間に75m進むペースで15分間歩いた距離を求めます。速さと時間を掛け合わせることで、全体の距離が計算できます。

歩く速度3

問題3

問題文の情報：距離 = 1800m、速さ = 分速90m
求めるもの：時間
使用する公式：時間 = 距離 ÷ 速さ

計算：1800 ÷ 90 = 20

答え：20分

解説：1分間に90m進むペースで1800mを歩くのにかかる時間を求めます。全体の距離を1分あたりの距離（速さ）で割ることで、必要な時間が計算できます。

これらの基本問題を通じて、速さ、距離、時間の関係性を理解し、適切な公式を選択して解く練習ができます。

関連記事：数学嫌いでも好きになれる！アッと驚く数学の面白エピソード！

応用問題

走行中の車

ここからは応用問題に挑戦していきましょう！難しく思えるかもしれませんが、基本的な考え方は同じです。

問題1：時速18kmで走る自動車が2時間15分かかる道のりは何kmですか？

問題2：100mを太郎君は11.5秒、花子さんは13秒で走ります。太郎君が花子さんの15m後ろから同時に同じ方向に走るとき、太郎君は花子さんに何秒後に追いつきますか？

解説

問題1

まず、問題文の情報を整理します。

速さ：時速18km
時間：2時間15分 = 2.25時間
求めるもの：距離
使用する公式：距離 = 速さ × 時間

計算：18 × 2.25 = 40.5

答え：40.5km

解説：この問題では、時間が2時間15分と与えられています。計算を簡単にするために、これを小数で表現します。
15分は1時間の1/4なので、2時間15分 = 2 + 0.25 = 2.25時間となります。
あとは、速さ（18km/h）と時間（2.25h）を掛け合わせるだけです。
18 × 2.25 = 40.5 となり、答えは40.5kmとなります。

競争する男女